
Inverse Trigonometric Functions
Let cos − 1 (2 3 ) = x, where x ∈ 0, π Then, cos x = 2 3 = cos 6 π ⇒ x = 6 π Solve any question of Inverse Trigonometric Functions with entering 2sin1−3√2cos1 2√3 closed edit asked 1926 0100 Anonymous if sin and cos are next to an absolute value, should I do sin*abs(x) or sin(abs(x) ?
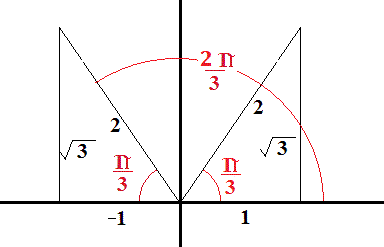
Cos^-1(- root 3 /2)
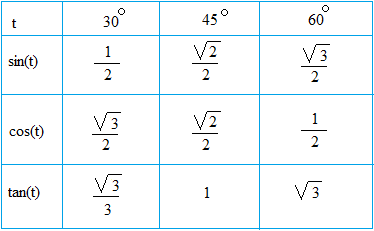
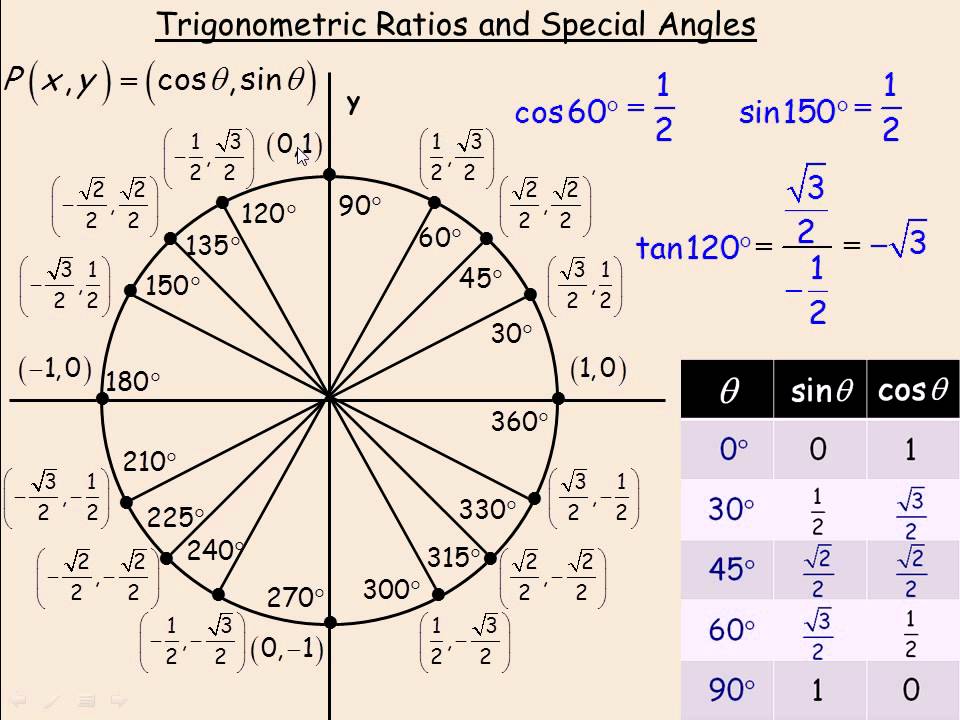
Cos^-1(- root 3 /2)-Eg 1 cos 30° = 1 Cos 30° = 1 x √3/2 = √3/2 Also, sin (90 θ) = cos θ and Cos (90 θ) = sin θ Also remember sin 45 = cos 45 = 1/√2 The value of sin θAre solved by group of students and teacher of Class 12, which is also the largest student community of Class 12 If the answer is not available please wait for a while and a community member will

Ex 2 1 11 Find Value Tan 1 1 Cos 1 1 2 Sin 1 1 2
N ∈ Z => θ = 2nπ ± (π/6) ;Extended Keyboard Examples Upload Random Compute answers using Wolfram's breakthrough technology & knowledgebase, relied on by millions of students & professionals For math, science, nutrition, history, geography, engineering, mathematics, linguistics, sports, finance, musicTan Inverse 1 By 3 Plus Tan Inverse 1 By 7 Plus Tan Inverse 1 By 13 Plus Tan Inverse 1 By 9703 Equal Tan Of Pi 4 1 2 Cos Inverse A B Plus Tan Pi 4 tan 1 (√3) cot 1 (√3) is equal to
People as Resource MCQEdit retag flag offensive reopen merge delete Closed for the following reason not a real question by IguananautSolution for Evaluate exacly cos1(√3/2) Q The four cases in which we can solve a triangle are ASA SSA SAS SSS(a) In which of these cases A a) The Law of Sines is most useful when you know a side, a, and the angle, A, opposite it Then for
Cos^-1(- root 3 /2)のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
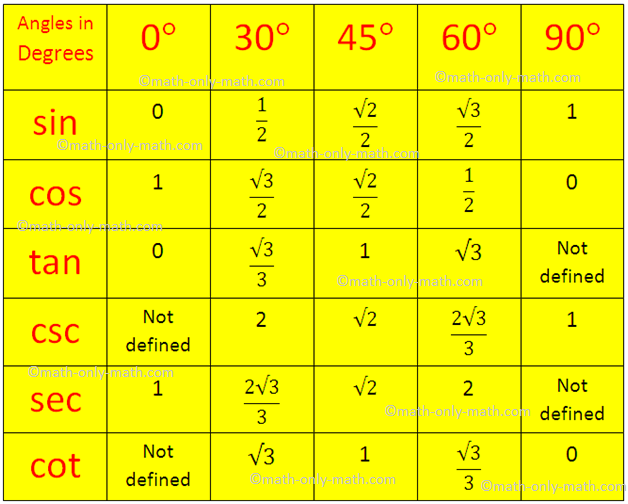
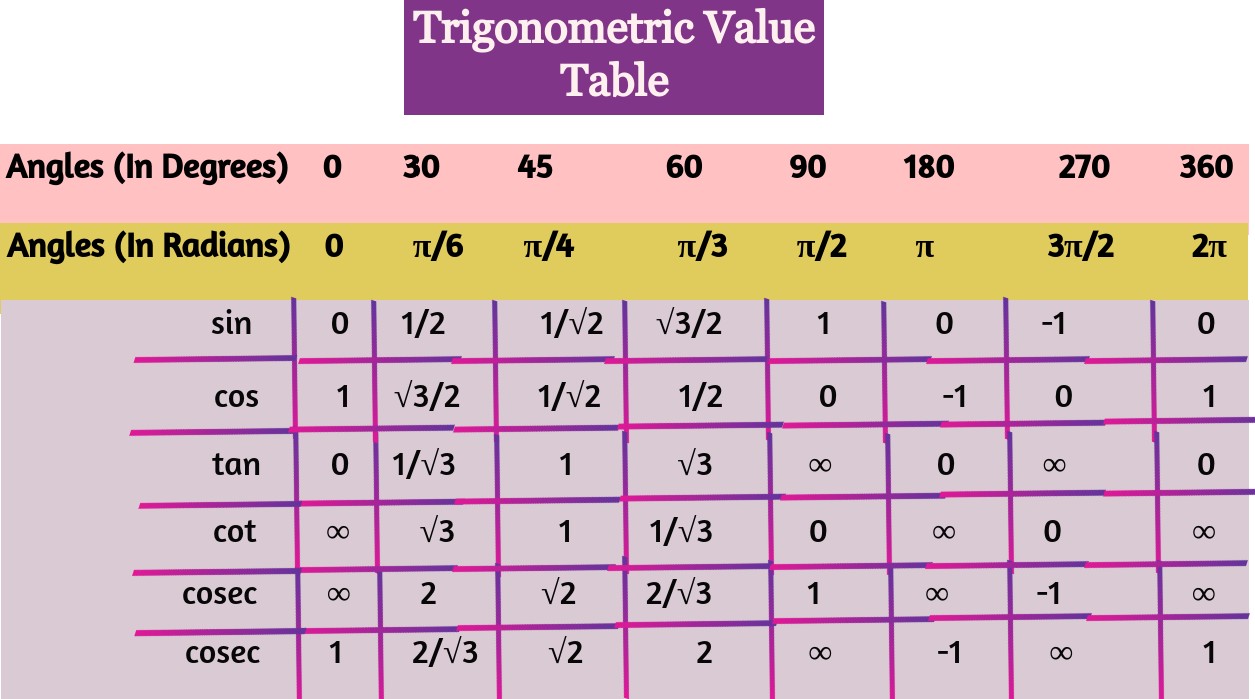 Trigonometric Table Toppers Bulletin |  Trigonometric Table Toppers Bulletin | 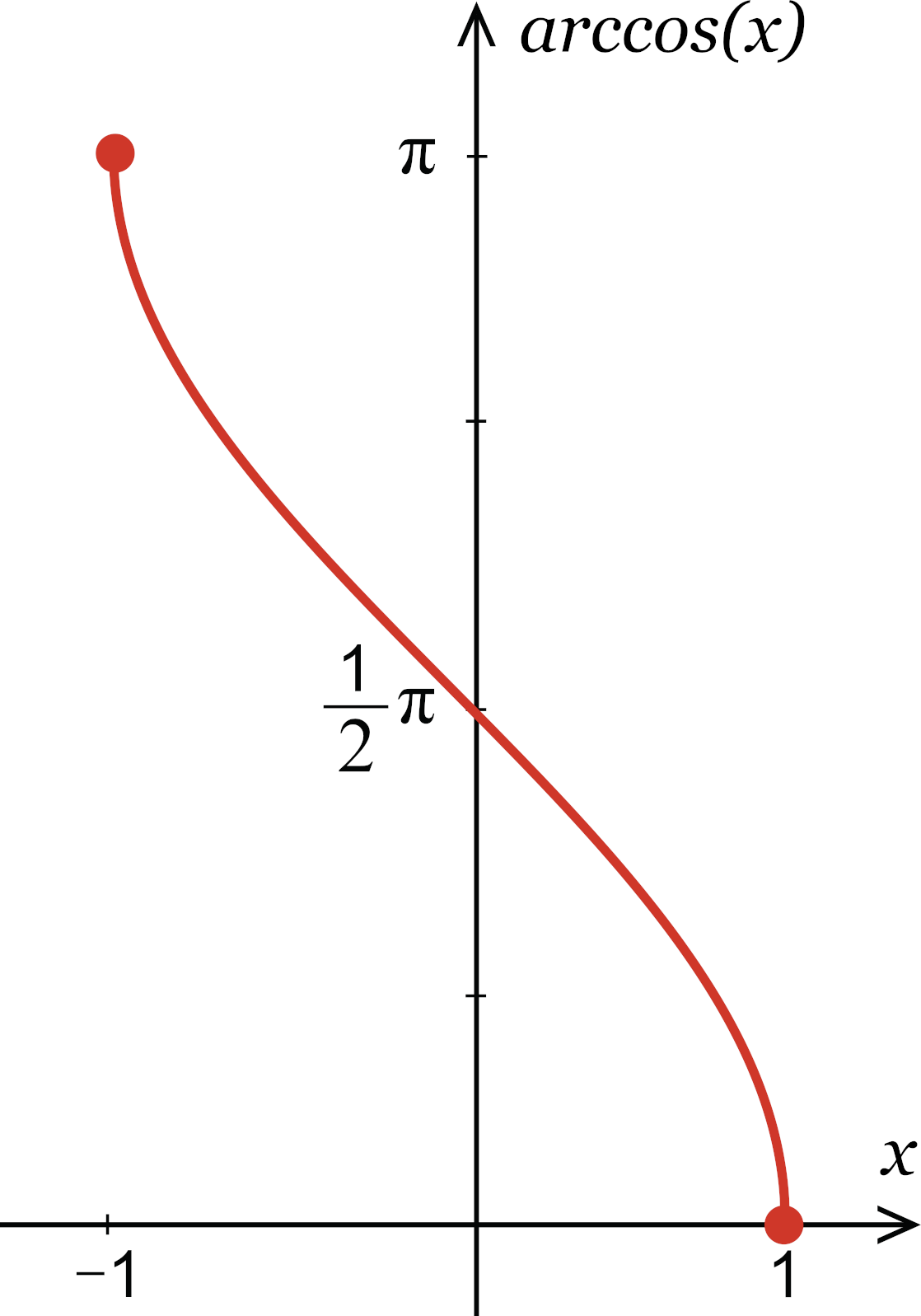 Trigonometric Table Toppers Bulletin |
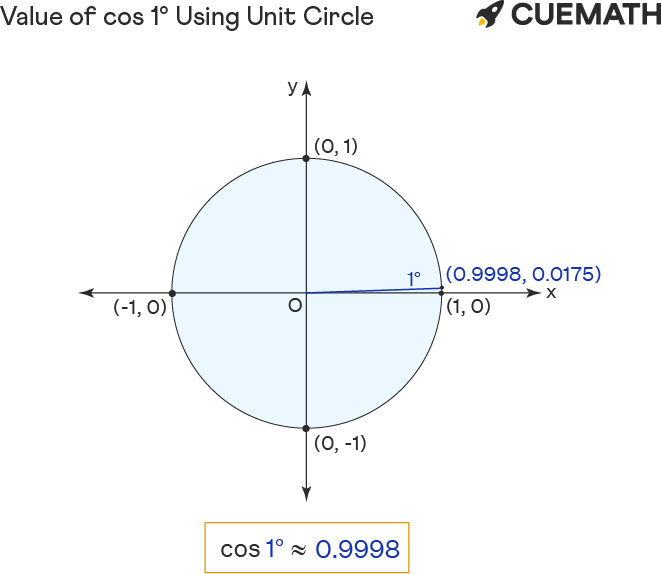 Trigonometric Table Toppers Bulletin |  Trigonometric Table Toppers Bulletin |  Trigonometric Table Toppers Bulletin |
 Trigonometric Table Toppers Bulletin |  Trigonometric Table Toppers Bulletin | 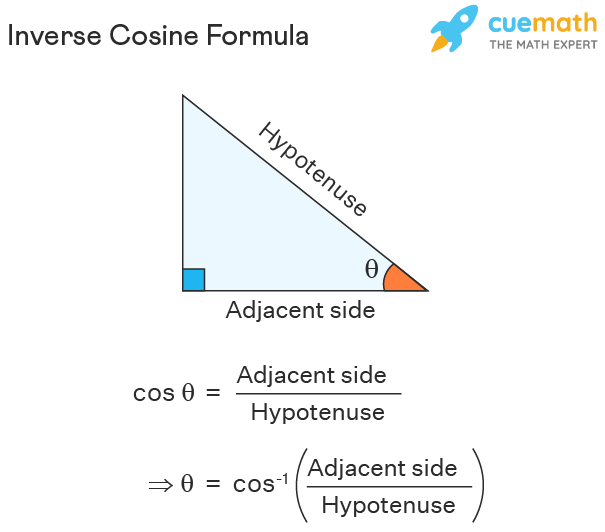 Trigonometric Table Toppers Bulletin |
 Trigonometric Table Toppers Bulletin | Trigonometric Table Toppers Bulletin |  Trigonometric Table Toppers Bulletin |
 Trigonometric Table Toppers Bulletin |  Trigonometric Table Toppers Bulletin |  Trigonometric Table Toppers Bulletin |
 Trigonometric Table Toppers Bulletin |  Trigonometric Table Toppers Bulletin |  Trigonometric Table Toppers Bulletin |
Trigonometric Table Toppers Bulletin |  Trigonometric Table Toppers Bulletin |  Trigonometric Table Toppers Bulletin |
 Trigonometric Table Toppers Bulletin |  Trigonometric Table Toppers Bulletin |  Trigonometric Table Toppers Bulletin |
 Trigonometric Table Toppers Bulletin |  Trigonometric Table Toppers Bulletin |  Trigonometric Table Toppers Bulletin |
Trigonometric Table Toppers Bulletin |  Trigonometric Table Toppers Bulletin | Trigonometric Table Toppers Bulletin |
Trigonometric Table Toppers Bulletin |  Trigonometric Table Toppers Bulletin |  Trigonometric Table Toppers Bulletin |
 Trigonometric Table Toppers Bulletin |  Trigonometric Table Toppers Bulletin |  Trigonometric Table Toppers Bulletin |
 Trigonometric Table Toppers Bulletin |  Trigonometric Table Toppers Bulletin | Trigonometric Table Toppers Bulletin |
 Trigonometric Table Toppers Bulletin |  Trigonometric Table Toppers Bulletin |  Trigonometric Table Toppers Bulletin |
 Trigonometric Table Toppers Bulletin | Trigonometric Table Toppers Bulletin |  Trigonometric Table Toppers Bulletin |
 Trigonometric Table Toppers Bulletin | Trigonometric Table Toppers Bulletin |  Trigonometric Table Toppers Bulletin |
Trigonometric Table Toppers Bulletin |  Trigonometric Table Toppers Bulletin | Trigonometric Table Toppers Bulletin |
Trigonometric Table Toppers Bulletin |  Trigonometric Table Toppers Bulletin |  Trigonometric Table Toppers Bulletin |
 Trigonometric Table Toppers Bulletin |  Trigonometric Table Toppers Bulletin |  Trigonometric Table Toppers Bulletin |
Trigonometric Table Toppers Bulletin | 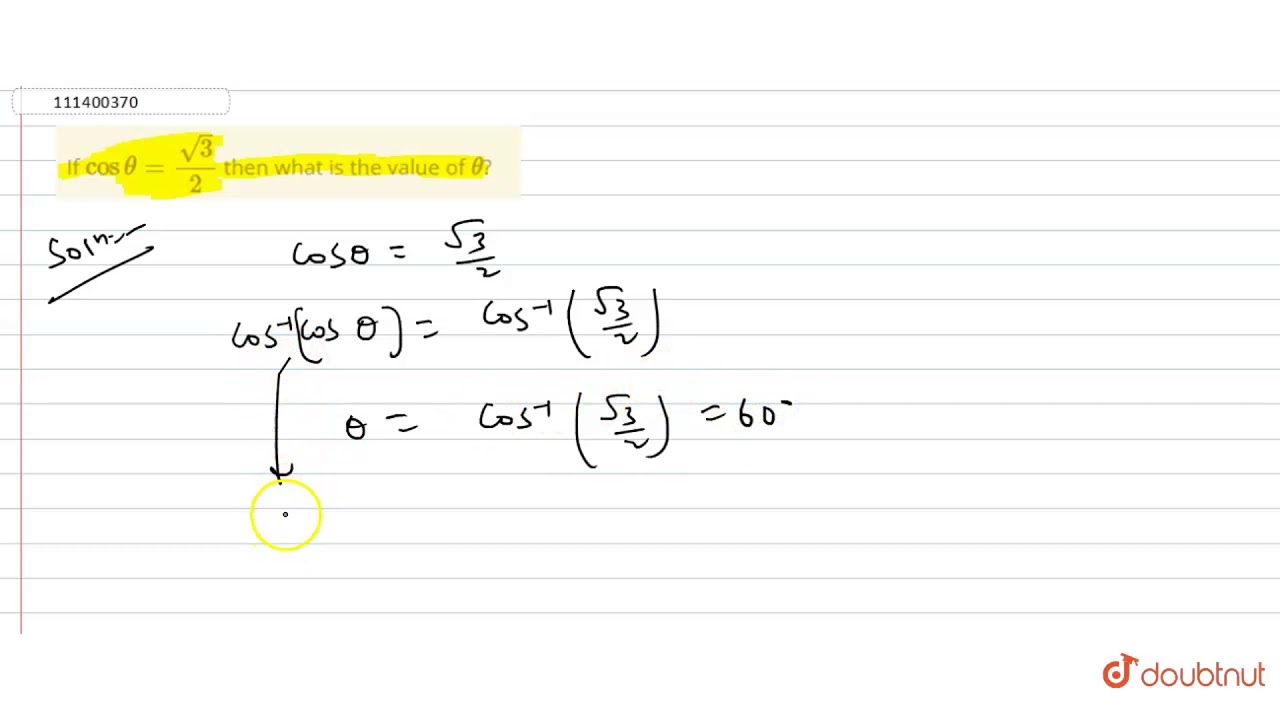 Trigonometric Table Toppers Bulletin |  Trigonometric Table Toppers Bulletin |
 Trigonometric Table Toppers Bulletin | Trigonometric Table Toppers Bulletin |  Trigonometric Table Toppers Bulletin |
 Trigonometric Table Toppers Bulletin | Trigonometric Table Toppers Bulletin |  Trigonometric Table Toppers Bulletin |
 Trigonometric Table Toppers Bulletin |  Trigonometric Table Toppers Bulletin |  Trigonometric Table Toppers Bulletin |
Trigonometric Table Toppers Bulletin |  Trigonometric Table Toppers Bulletin | 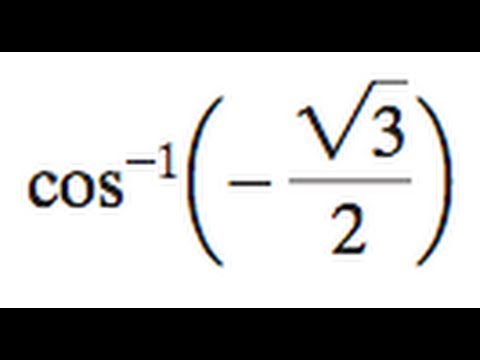 Trigonometric Table Toppers Bulletin |
 Trigonometric Table Toppers Bulletin |  Trigonometric Table Toppers Bulletin | Trigonometric Table Toppers Bulletin |
 Trigonometric Table Toppers Bulletin |  Trigonometric Table Toppers Bulletin |  Trigonometric Table Toppers Bulletin |
 Trigonometric Table Toppers Bulletin | Trigonometric Table Toppers Bulletin | 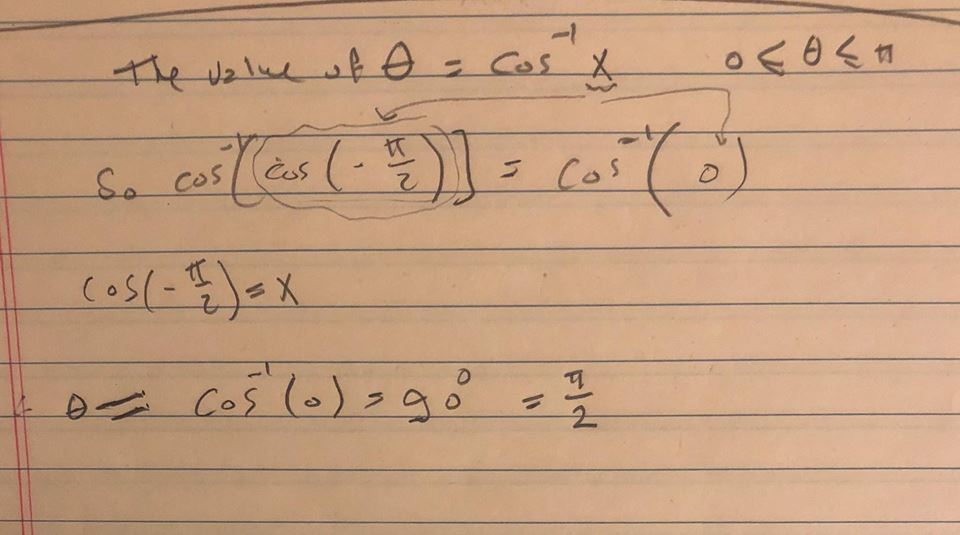 Trigonometric Table Toppers Bulletin |
 Trigonometric Table Toppers Bulletin | Trigonometric Table Toppers Bulletin |  Trigonometric Table Toppers Bulletin |
 Trigonometric Table Toppers Bulletin |  Trigonometric Table Toppers Bulletin |  Trigonometric Table Toppers Bulletin |
 Trigonometric Table Toppers Bulletin |  Trigonometric Table Toppers Bulletin |  Trigonometric Table Toppers Bulletin |
Trigonometric Table Toppers Bulletin |  Trigonometric Table Toppers Bulletin |  Trigonometric Table Toppers Bulletin |
 Trigonometric Table Toppers Bulletin |  Trigonometric Table Toppers Bulletin |  Trigonometric Table Toppers Bulletin |
 Trigonometric Table Toppers Bulletin |  Trigonometric Table Toppers Bulletin |  Trigonometric Table Toppers Bulletin |
 Trigonometric Table Toppers Bulletin |  Trigonometric Table Toppers Bulletin |  Trigonometric Table Toppers Bulletin |
 Trigonometric Table Toppers Bulletin | Trigonometric Table Toppers Bulletin |
Ehendricks8 ehendricks8 Mathematics High School answered This question is asking you "what angle gives you a cos of square root 3/2"?Should sin * be sin( ?
Incoming Term: cos^-1(-3/2), cos inverse 3/2, cos^-1(2x-3) domain, cos^-1(-sqrt 3/2), cos^-1(- root 3 /2), cos inverse 2/3 value, 1/cos^2x-(3+√3)tan3x+√3=0, cos inverse 2pi/3, cos 1/3 akar 2 berapa derajat, cos 1/3 akar 2,




0 件のコメント:
コメントを投稿